SMITH CHART
Smith chart, diciptakan oleh Phillip H. Smith (1905-1987), adalah bantuan grafis atau nomogram yang dirancang untuk membantu electrical engineer yang dalam bidang frekuensi radio (RF) dalam memecahkan masalah dengan jalur transmisi dan pencocokan sirkuit. Penggunaan utilitas diagram Smith terus berkembang selama bertahun-tahun dan masih banyak digunakan saat ini, tidak hanya sebagai bantuan pemecahan masalah, tetapi sebagai demonstrasi grafis dari berapa banyak parameter RF berlaku pada satu atau lebih frekuensi, alternatif untuk menggunakan tabel informasi. Bagan Smith dapat digunakan untuk mewakili parameter, termasuk impedansi , admittances ,koefisien refleksi ,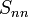 scattering
parameters, noise figure circles, constant gain contours and regions
for unconditional stability. Diagram Smith yang paling sering digunakan
pada atau di dalam radius unity.
scattering
parameters, noise figure circles, constant gain contours and regions
for unconditional stability. Diagram Smith yang paling sering digunakan
pada atau di dalam radius unity.Karakteristik Matematis
Actual and normalised impedance and admittance
Sebuah saluran transmisi dengan impedansi karakteristik 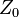 secara universal dianggap memiliki karakteristik masuk dari
secara universal dianggap memiliki karakteristik masuk dari  dimana
dimana
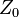 secara universal dianggap memiliki karakteristik masuk dari
secara universal dianggap memiliki karakteristik masuk dari  dimana
dimana- Setiap impedansi,
 dinyatakan
dalam ohm, dapat dinormalisasi dengan membaginya dengan impedansi
karakteristik, sehingga impedansi ternormalisasi dengan menggunakan
huruf kecil z, dapat dihitung dengan:
dinyatakan
dalam ohm, dapat dinormalisasi dengan membaginya dengan impedansi
karakteristik, sehingga impedansi ternormalisasi dengan menggunakan
huruf kecil z, dapat dihitung dengan:
Sedangkan admitansi ternormalisasi adalah

-
-
-
Impedansi ternormalisasiSmith Chart untuk
Menggunakan teori saluran transmisi, jika jalur transmisi dihentikan di sebuah impedansi ( ) Yang berbeda dari impedansi karakteristik (
) Yang berbeda dari impedansi karakteristik ( 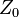 ), Sebuah gelombang berdiri akan terbentuk pada saluran terdiri dari resultan (
), Sebuah gelombang berdiri akan terbentuk pada saluran terdiri dari resultan (  ) dan (
) dan (  ). Menggunakan kompleks eksponensial notasi:dimana,
). Menggunakan kompleks eksponensial notasi:dimana, dan
dan
 adalah temporal bagian dari gelombang
adalah temporal bagian dari gelombang adalah bagian ruang dari gelombang dan
adalah bagian ruang dari gelombang dan
 adalah frekuensi sudut dalam radian per detik (rad / s)
adalah frekuensi sudut dalam radian per detik (rad / s) adalah frekuensi dalam hertz (Hz)
adalah frekuensi dalam hertz (Hz) adalah waktu dalam detik (s)
adalah waktu dalam detik (s) dan
dan 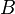 adalah konstanta
adalah konstanta adalah jarak diukur sepanjang garis transmisi dari generator dalam meter (m)
adalah jarak diukur sepanjang garis transmisi dari generator dalam meter (m)
 adalah konstanta propagasi yang memiliki unit 1 / m
adalah konstanta propagasi yang memiliki unit 1 / m
dimana adalah konstanta atenuasi dalam nepers per meter (Np / m)
adalah konstanta atenuasi dalam nepers per meter (Np / m) adalah fase konstan dalam radian per meter (rad / m)
adalah fase konstan dalam radian per meter (rad / m)
Diagram Smith digunakan dengan satu frekuensi pada suatu waktu sehingga bagian temporal fase ( ) Adalah tetap. Semua istilah yang sebenarnya dikalikan dengan ini untuk mendapatkan fasa sesaat , tetapi konvensional dan dipahami untuk menghilangkan itu. Oleh karena itu:
) Adalah tetap. Semua istilah yang sebenarnya dikalikan dengan ini untuk mendapatkan fasa sesaat , tetapi konvensional dan dipahami untuk menghilangkan itu. Oleh karena itu: dan
dan
Variasi koefisien refleksi kompleks dengan posisi sepanjang garis
Refleksi koefisien tegangan kompleks didefinisikan sebagai rasio dari gelombang tercermin pada kejadian (atau maju) gelombang. Oleh karena itudi mana C adalah juga sebuah konstanta.Untuk jalur transmisi seragam (di mana
didefinisikan sebagai rasio dari gelombang tercermin pada kejadian (atau maju) gelombang. Oleh karena itudi mana C adalah juga sebuah konstanta.Untuk jalur transmisi seragam (di mana konstan), refleksi kompleks koefisien gelombang berdiri bervariasi sesuai dengan posisi di telepon. Jika garis adalah lossy (
konstan), refleksi kompleks koefisien gelombang berdiri bervariasi sesuai dengan posisi di telepon. Jika garis adalah lossy (  adalah terbatas) ini diwakili pada diagram Smith oleh spiral path. Dalam masalah Smith paling chart Namun, kerugian dapat diasumsikan diabaikan (
adalah terbatas) ini diwakili pada diagram Smith oleh spiral path. Dalam masalah Smith paling chart Namun, kerugian dapat diasumsikan diabaikan ( 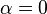 ) Dan tugas pemecahan mereka adalah sangat disederhanakan. Untuk kasus hilangnya bebas sehingga, istilah untuk refleksi koefisien kompleks menjadikonstanta
) Dan tugas pemecahan mereka adalah sangat disederhanakan. Untuk kasus hilangnya bebas sehingga, istilah untuk refleksi koefisien kompleks menjadikonstanta juga dapat ditulis sebagaimana
juga dapat ditulis sebagaimana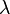 merupakan panjang gelombang dalam saluran transmisi pada frekuensi uji.Oleh karena ituPersamaan ini menunjukkan bahwa, untuk gelombang berdiri, refleksi koefisien kompleks dan impedansi berulang setiap panjang gelombang setengah sepanjang saluran transmisi.Refleksi koefisien kompleks umumnya hanya disebut sebagai koefisien refleksi. Skala keliling luar diagram Smith merupakan jarak dari generator untuk skala beban pada panjang gelombang dan karena itu skala dari nol sampai 0,50.
merupakan panjang gelombang dalam saluran transmisi pada frekuensi uji.Oleh karena ituPersamaan ini menunjukkan bahwa, untuk gelombang berdiri, refleksi koefisien kompleks dan impedansi berulang setiap panjang gelombang setengah sepanjang saluran transmisi.Refleksi koefisien kompleks umumnya hanya disebut sebagai koefisien refleksi. Skala keliling luar diagram Smith merupakan jarak dari generator untuk skala beban pada panjang gelombang dan karena itu skala dari nol sampai 0,50.
Variasi impedansi ternormalisasi dengan posisi sepanjang garis
Jika  dan
dan  adalah tegangan dan arus masuk terminasi pada akhir saluran transmisi masing-masing, maka
adalah tegangan dan arus masuk terminasi pada akhir saluran transmisi masing-masing, maka
 dan
dan  adalah tegangan dan arus masuk terminasi pada akhir saluran transmisi masing-masing, maka
adalah tegangan dan arus masuk terminasi pada akhir saluran transmisi masing-masing, maka dan
dan .
.
Dengan membagi persamaan ini dan menggantikannya untuk kedua koefisien refleksi tegangan
dan impedansi dinormalisasi pengakhiran yang diwakili oleh huruf kecil z, T subscript
memberikan hasil:
 .
.
Atau, dalam hal refleksi koefisien
Ini adalah persamaan yang digunakan untuk membangun tabel Z Smith. Secara matematis berbicara  dan
dan  terkait melalui transformasi Möbius .
terkait melalui transformasi Möbius .
 dan
dan  terkait melalui transformasi Möbius .
terkait melalui transformasi Möbius .
Baik  dan
dan  disajikan dalam bilangan kompleks tanpa unit. Mereka
berdua berubah dengan frekuensi sehingga untuk setiap pengukuran
khusus, frekuensi yang dilakukan harus dinyatakan bersama-sama dengan
impedansi karakteristik.
disajikan dalam bilangan kompleks tanpa unit. Mereka
berdua berubah dengan frekuensi sehingga untuk setiap pengukuran
khusus, frekuensi yang dilakukan harus dinyatakan bersama-sama dengan
impedansi karakteristik.
 dan
dan  disajikan dalam bilangan kompleks tanpa unit. Mereka
berdua berubah dengan frekuensi sehingga untuk setiap pengukuran
khusus, frekuensi yang dilakukan harus dinyatakan bersama-sama dengan
impedansi karakteristik.
disajikan dalam bilangan kompleks tanpa unit. Mereka
berdua berubah dengan frekuensi sehingga untuk setiap pengukuran
khusus, frekuensi yang dilakukan harus dinyatakan bersama-sama dengan
impedansi karakteristik. dapat dinyatakan dalam besaran dan sudut pada diagram polar . Setiap refleksi aktual koefisien harus memiliki besarnya kurang dari atau sama dengan kesatuan demikian, pada frekuensi uji, ini mungkin dinyatakan dengan sebuah titik di dalam lingkaran radius persatuan. Diagram Smith sebenarnya dibangun di atas seperti diagram polar. The
scaling diagram Smith dirancang sedemikian rupa sehingga koefisien
refleksi dapat dikonversi menjadi impedansi ternormalisasi atau
sebaliknya. Menggunakan grafik Smith, impedansi normalisasi
dapat diperoleh dengan akurasi yang cukup dengan memetakan titik
mewakili koefisien refleksi memperlakukan diagram Smith sebagai diagram kutub dan kemudian membaca nilainya langsung dengan menggunakan skala Smith grafik karakteristik. Teknik ini merupakan alternatif grafis untuk mengganti nilai-nilai dalam persamaan.
dapat dinyatakan dalam besaran dan sudut pada diagram polar . Setiap refleksi aktual koefisien harus memiliki besarnya kurang dari atau sama dengan kesatuan demikian, pada frekuensi uji, ini mungkin dinyatakan dengan sebuah titik di dalam lingkaran radius persatuan. Diagram Smith sebenarnya dibangun di atas seperti diagram polar. The
scaling diagram Smith dirancang sedemikian rupa sehingga koefisien
refleksi dapat dikonversi menjadi impedansi ternormalisasi atau
sebaliknya. Menggunakan grafik Smith, impedansi normalisasi
dapat diperoleh dengan akurasi yang cukup dengan memetakan titik
mewakili koefisien refleksi memperlakukan diagram Smith sebagai diagram kutub dan kemudian membaca nilainya langsung dengan menggunakan skala Smith grafik karakteristik. Teknik ini merupakan alternatif grafis untuk mengganti nilai-nilai dalam persamaan.
Dengan
menggantikan ekspresi untuk perubahan koefisien refleksi bagaimana
sepanjang jalur transmisi kerugian tak tertandingi gratis
atas kerugian kasus bebas, ke dalam persamaan untuk impedansi dinormalisasi dalam hal refleksi koefisien
 .
.
dan menggunakan identitas Euler's
menghasilkan versi impedansi saluran transmisi persamaan untuk bebas kasus hilangnya: [8]
mana  adalah impedansi 'terlihat' pada masukan dari garis hilangnya transmisi bebas dari l panjang, diakhiri dengan sebuah impedansi
adalah impedansi 'terlihat' pada masukan dari garis hilangnya transmisi bebas dari l panjang, diakhiri dengan sebuah impedansi 
 adalah impedansi 'terlihat' pada masukan dari garis hilangnya transmisi bebas dari l panjang, diakhiri dengan sebuah impedansi
adalah impedansi 'terlihat' pada masukan dari garis hilangnya transmisi bebas dari l panjang, diakhiri dengan sebuah impedansi 
Versi
persamaan garis penularan bisa juga diturunkan untuk hilangnya
pengakuan kasus bebas dan untuk kasus-kasus impedansi dan masuk lossy.
Bagan Smith setara grafis menggunakan persamaan saluran transmisi adalah untuk menormalkan  ,
Untuk plot titik yang dihasilkan pada grafik Smith Z dan untuk membuat
lingkaran melalui titik berpusat di pusat diagram Smith. Jalan sepanjang busur lingkaran mewakili bagaimana perubahan impedansi sementara bergerak sepanjang saluran transmisi.Dalam
hal ini skala (panjang gelombang) melingkar harus digunakan, mengingat
bahwa ini adalah panjang gelombang dalam saluran transmisi dan mungkin
berbeda dari panjang gelombang ruang bebas.
,
Untuk plot titik yang dihasilkan pada grafik Smith Z dan untuk membuat
lingkaran melalui titik berpusat di pusat diagram Smith. Jalan sepanjang busur lingkaran mewakili bagaimana perubahan impedansi sementara bergerak sepanjang saluran transmisi.Dalam
hal ini skala (panjang gelombang) melingkar harus digunakan, mengingat
bahwa ini adalah panjang gelombang dalam saluran transmisi dan mungkin
berbeda dari panjang gelombang ruang bebas.
 ,
Untuk plot titik yang dihasilkan pada grafik Smith Z dan untuk membuat
lingkaran melalui titik berpusat di pusat diagram Smith. Jalan sepanjang busur lingkaran mewakili bagaimana perubahan impedansi sementara bergerak sepanjang saluran transmisi.Dalam
hal ini skala (panjang gelombang) melingkar harus digunakan, mengingat
bahwa ini adalah panjang gelombang dalam saluran transmisi dan mungkin
berbeda dari panjang gelombang ruang bebas.
,
Untuk plot titik yang dihasilkan pada grafik Smith Z dan untuk membuat
lingkaran melalui titik berpusat di pusat diagram Smith. Jalan sepanjang busur lingkaran mewakili bagaimana perubahan impedansi sementara bergerak sepanjang saluran transmisi.Dalam
hal ini skala (panjang gelombang) melingkar harus digunakan, mengingat
bahwa ini adalah panjang gelombang dalam saluran transmisi dan mungkin
berbeda dari panjang gelombang ruang bebas.
Menggunakan Smith Chart
Pada
dasarnya, bagian dalam lingkaran dipergunakan untuk menghitung
impedansi dan admitansi. Sub bagian dari impedansi adalah resistansi dan
reaktansi (Z = R + jX). Sementara itu, sub bagian dari admitansi adalah
konduktansi dan suseptansi (Y = G + jB).
Lingkaran-lingkaran
dalam Smith Chart menunjukkan besarnya resistansi. Resistansi bernilai
nol dimulai dari kiri, resistansi bernilai satu tepat di titik tengah,
dan bernilai sangat besar di sisi kanan (pada grafik hanya terbaca
sampai lima puluh). Nilai resistansi sama pada satu lingkaran yang sama.
Adapun
garis-garis dalam Smith Chart menunjukkan besarnya reaktansi. Reaktansi
bernilai nol adalah garis lurus sumbu resistansi, dan semakin ke kanan
akan semakin besar nilainya. Garis-garis bagian atas sumbu resistansi
adalah untuk reaktansi bernilai positif, sementara bagian bawah sumbu
resistansi adalah untuk reaktansi bernilai negatif.
Nilai
total dari resistansi dan reaktansi tersebut kita namakan impedansi
(tahanan kompleks) yang memiliki satuan ohm. Untuk memodelkan sebuah
impedansi ke dalam Smith Chart, kita harus melakukan normalisasi
terhadap nilai impedansi tersebut jika nilai-nilai besaran impedansi
tersebut tidak termuat dalam skala Smith Chart. Nilai normalisasi bebas
asalkan nilai-nilai hasil normalisasi tersebut dapat kita
modelkan/gambarkan dalam Smith Chart.
Misalkan,
kita memiliki impedansi dengan nilai Z = (100 + j50) ohm. Di dalam
grafik, tidak terdapat angka 100, nilai tersebut terlalu besar untuk
dimodelkan langsung. Oleh karena itu, kita harus melakukan normalisasi
dengan 50 misalnya, sehingga nilai Z normalisasi = (2 + j1) ohm.
Sesuai dengan kaidah reaktansi, induktor dan kapasitor akan menjadi hambatan imajiner jika diberi arus bolak-balik atau AC (Alternate Current).
Nilai reaktansi induktif (XL) didapat dari jwL = j*2*phi*L. Sedangkan,
nilai reaktansi kapasitif (XC) didapat dari 1/(jwC) = -j/(wC). Sehingga
dapat disimpulkan bahwa, reaktansi induktif bernilai positif dan berada
di atas sumbu resistansi. Di sisi lain, reaktansi kapasitif bernilai
negatif sehingga berada di bawah sumbu resistansi.
Pada
lingkaran (nilai resistansi) yang sama, jika ditambahkan induktor
secara seri, maka ia akan bergerak searah jarum jam (semakin ke
atas/membesar). Sedangkan, jika ditambahkan kapasitor secara seri, maka
ia akan bergerak berlawanan arah jarum jam (semakin ke bawah/mengecil).
sumber :http://elmag001.blogspot.co.id/2011/04/smith-chart.html












Tidak ada komentar:
Posting Komentar